Kali ini kita akan membahas mengenai dimensi tiga, dengan pokok bahasannya adalah jarak dalam ruang. Pada materi ini, kita membahas mengenai jarak dari objek-objek dalam ruang seperti titik, garis, dan bidang.
Pelajari materi Teorema Pythagoras sebagai materi prasyarat.
A. Unsur-unsur Ruang
1. Titik
Titik merupakan objek geometri terkecil yang dapat kita amati.
2. Garis
Garis merupakan objek geometri yang panjang tak terhingga, lurus, dan tidak memiliki lebar.
Ruas garis adalah sebagian dari garis yang
dibatasi oleh dua titik ujung yang berbeda, dan memuat semua titik pada garis
di antara ujung-ujungnya.
3. Bidang
Bidang adalah permukaan rata yang meluas ke
segala arah,tak terbatas, terus-menerus dalam semua arah, dan tidak memiliki
ketebalan.Bidang adalah himpunan titik-titik yang memiliki luas tak terhingga.
Titik : titik A, B, C, D, E, F, G, H
Garis : AB, AC, AD, BC, BD, AG, AE, AH,dan seterusnya.
Bidang : Bidang ABCD, BCGF, ADHE, EFGH, BDHF,
ACGE, ACH, BDG, dan seterusnya.
B. Jarak Dalam Ruang
Sebelumnya, apa itu jarak? Jarak adalah panjang ruas garis terpendek yang menghubungkan kedua objek geometri (Titik, Garis, dan Bidang).
1. Titik ke Titik
Terdapat dua kondisi yang mungkin terjadi jika menghubungkan dua titik.
Titik
berimpit dengan titik
Titik A dan Titik B terletak pada titik yang sama, sehingga jarak titik A ke titik B adalah 0.
Titik tidak berimpit dengan titik
Titik A dan titik B tidak berimpit sehingga, jarak kedua titik tidak 0.
Jarak titik A ke titik B sama dengan panjang ruas garis d, atau AB.
Misalkan panjang rusuk kubus adalah s.
a. Jarak antara dua titik yang sama dengan panjang rusuk kubus
Jarak titik A ke titik B sama dengan panjang rusuk kubus yaitu S. Hal ini juga berlaku untuk: BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, dan DH.
b. Jarak antara dua titik yang sama dengan diagonal sisi kubus
Jarak titik A ke titik F sama dengan panjang diagonal sisi ABFE.
Hal ini juga berlaku untuk BE, BG, FC, dan diagonal sisi lainnya.
c. Jarak antara dua titik yang sama dengan diagonal ruang kubus
Jarak titik A ke titik G sama dengan panjang diagonal ruang kubus ABCD.EFGH.
Hal ini juga berlaku untuk BH, CE, dan DF.
d. Jarak antara dua titik lainnya
Pada dasarnya menentukan jarak dua titik dapat menggunakan Teorema Pythagoras. Sebelum menerapkan rumus pada Teorema Pythagoras, terlebih dahulu tentukan segitiga siku-siku yang memuat dua titik yang akan dihitung jaraknya. Contoh:
Jika panjang rusuk kubus diatas adalah 6 cm dan titik T tepat di tengah HG, maka cara menentukan jarak titik T ke titik E adalah sebagai berikut:
1. Tentukan segitiga yang memuat titik T dan titik E
2. Terapkan Teorema Pythagoras pada segitiga ETH
Selain jarak titik T ke titik E, mari kita hitung jarak titik T ke titik A
1. Tentukan segitiga yang memuat titik T dan titik A
AH adalah diagonal sisi pada sisi ADHE
2. Terapkan Teorema Pythagoras pada segitiga ATH
Pelajari juga :
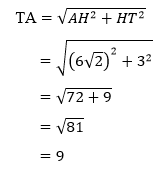
Tidak ada komentar:
Posting Komentar